9. Les algorithmes de placement¶
Les algorithmes de placement permettent d'attribuer des coordonnées cartésiennes non géographiques (i,j) à chaque nœud du graphe ce qui rend possible leur représentation graphique.
On distingue deux grandes catégories d'algorithmes. Les premiers exploitent des graphes orientés (GO) pour lesquels les arêtes ont un sens de parcours bien précis (les arêtes s'appelent alors des arcs), alors que les seconds considèrent que les arêtes ne sont pas d'orientation (GNO).
Il en découle une organisation graphique différente, le nœud racine des graphes orientés étant généralement positionné en haut du graphe, alors qu'il occupe une position centrale (mais pas toujours) pour les graphes non orientés.
Les exemples produits à partir des algorithmes décrits ci-dessous ont tous été générés à partir du même jeu de données source représentant un réseau de distribution (arbre) de fibre télécom (FTTH).
Le nœud source fourni à l'algorithme (SRO-018-201) n'est pas le véritable nœud racine de l'arbre (NRO-82-026) ce qui permet d'illustrer certaines différences entre les algorithmes exploitant des graphes orientés (GO) et ceux exploitant des graphes non orientés (GNO).
Jeu de données source des exemples :
1-Arbre sur grille¶
Cet algorithme permet de positionner les nœuds d'un arbre sur une grille. L'identifiant du nœud racine doit être fourni et sert d'origine au dessin de l'arbre. Sinon, le premier noeud du graphe est utilisé comme noeud racine. Le graphe est considéré comme non orienté, tous les nœuds sont donc représentés quel que soit le nœud racine. C'est cet algorithme qui est utilisé par GraphLayouterForExcel.
Source : Veremes
Exemple de représentation avec Algorithme n°12-Circulaire¶
Cet algorithme permet de positionner les nœuds d'un graphe quelconque sur un cercle. Le nœud racine est positionné en haut du cercle. Le graphe est considéré comme non orienté, tous les nœuds sont donc représentés quel que soit le nœud racine.
Source : Veremes
Exemple de représentation avec Algorithme n°23-Circulaire Centre¶
Cet algorithme permet de positionner les nœuds d'un graphe quelconque sur un cercle. Le nœud racine est positionné au centre du cercle. Le graphe est considéré comme non orienté, tous les nœuds sont donc représentés quel que soit le nœud racine.
Source : Veremes
Exemple de représentation avec Algorithme n°34-Dot¶
Cet algorithme permet de positionner les nœuds d'un graphe orienté sous une forme arborescente. Le nœud racine est présenté en haut du graphe.
Source : Graphviz (consulter la documentation détaillée)
Exemple de représentation avec Algorithme n°45-Circulaire¶
Cet algorithme permet de positionner les nœuds d'un graphe quelconque sur un cercle. Le nœud racine est positionné en haut du cercle. Le graphe est considéré comme orienté, seul le nœud racine et les nœuds en aval du nœud sont représentés. Par rapport à l'algorithme 2-Circulaire qui donne un résutat comparable, 5-Circulaire minimise la longueur totale des arêtes en positionnant les noeuds de manière pertinente sur le cercle.
Source : Veremes
Exemple de représentation avec Algorithme n°56-Circulaire Centre¶
Cet algorithme permet de positionner les nœuds d'un graphe quelconque sur un cercle. Le nœud racine est positionné au centre du cercle. Le graphe est considéré comme orienté, seul le nœud racine et les nœuds en aval du nœud sont représentés. Par rapport à l'algorithme 3-Circulaire Centre qui donne un résutat comparable, 6-Circulaire Centre minimise la longueur totale des arêtes en positionnant les noeuds de manière pertinente sur le cercle.
Source : Veremes
Exemple de représentation avec Algorithme n°67-Radial¶
Cet algorithme permet de positionner les nœuds d'un graphe quelconque sur un ensemble de cercles concentriques. Le nœud racine est positionné au centre du graphe. Le graphe est considéré comme orienté, seul le nœud racine et les nœuds en aval du nœud sont représentés.
Source : Veremes
Exemple de représentation avec Algorithme n°78-Neato¶
Cet algorithme permet de positionner les nœuds d'un graphe non orienté quelconque. Le nœud racine est positionné au centre du graphe.
Source : Graphviz - Documentation
Exemple de représentation avec Algorithme n°89-Twopi (radial)¶
Cet algorithme permet de positionner les nœuds d'un graphe quelconque sur un ensemble de cercles concentriques. Le nœud racine est positionné au centre du graphe.
Source : Graphviz - Documentation
Exemple de représentation avec Algorithme n°910-Circo (circulaire)¶
Cet algorithme permet de positionner les nœuds d'un graphe quelconque selon un ensemble de cercles. Le nœud racine est positionné au centre du graphe. Le graphe est considéré comme orienté, seul le nœud racine et les nœuds en aval du nœud sont représentés.
Source : Graphviz - Documentation
Exemple de représentation avec Algorithme n°1011-FDP¶
Cet algorithme permet de positionner les nœuds d'un graphe non orienté quelconque. Le nœud racine est positionné au centre du graphe.
Source : Graphviz - Documentation
Exemple de représentation avec Algorithme n°1112-SFDP¶
Algorithme proche de FDP mais adapté à de larges jeux de données.
Source : Graphviz - Documentation
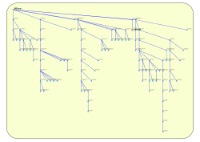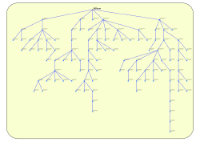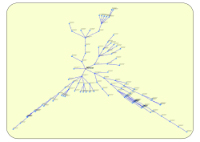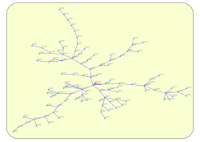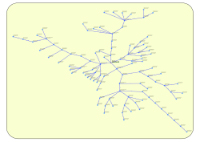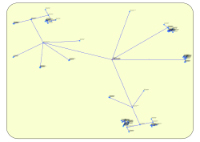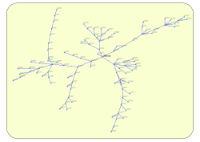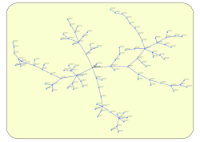Exemple de représentation avec Algorithme n°12